| III. Circuits logiques combinatoires | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Page d'accueil Plan : I. Les composants à semi-conducteurs 1. La diode 2. Le transistor bipolaire 3. Le transistor JFET II. Les différentes familles technologiques de circuits logiques 1. L'algèbre de Boole 2. Circuits logiques à éléments discrets 3. Circuits intégrés logiques DTL 4. Circuits intégrés logiques TTL 5. Circuits intégrés logiques C-MOS III. Circuits logiques combinatoires 1. Circuits multiplexeurs 2. Circuits démultiplexeurs et décodeurs 3. Circuits encodeurs 4. Circuits comparateurs et détecteurs d'égalité IV. Circuits logiques séquentiels 1. Bascule RS 2. Bascule D 3. Bascule D à déclenchement par front 4. Bascule JK et JK à déclenchement par front |
Un circuit logique est dit "combinatoire" quand aucune
sortie
n'est reliée à une entrée, c'est
à dire
quand le circuit est en boucle ouverte. Ainsi une sortie ne
dépend que de l'état des entrées. Page d'accueil Plan : 1. Circuits multiplexeurs 2. Circuits démultiplexeurs et décodeurs 3. Circuits encodeurs 4. Circuits comparateurs et détecteurs d'égalité 1. Circuits multiplexeurs Ces circuits ont 1 sortie. S'ils ont un nombre n de commandes, alors ils auront 2^n entrées. Dans notre exemple nous prendrons un multiplexeurs à 3 commandes (A, B et C) qui aura donc 2^3 = 8 entrées (D0, D1, ..., D7) et une sortie Y. Ce circuit est composé d'un NOR (NON OU), de 8 AND et de 8 INVERSEURS :  Table de vérité :
Fonctionnement : - si /G = 1 alors quelques soient la valeur des commandes A, B et C (0 ou 1) la sortie Y sera à 0 - si /G = 0 alors la sortie Y va dépendre de l'état des 3 commandes. Si dans notre commande à 3 bits, C est le bit de poids fort (valeur 2^2 = 4 en base 10) et A le bit de poids faible (valeur 2^0 = 1 en base 10) alors voilà comment varie Y : - si CBA = 000 en base 2 => 0 en base 10, alors la sortie Y va prendre la valeur (0 ou 1) de l'entrée D0. - si CBA = 001 en base 2 => 1 en base 10, alors la sortie Y va prendre la valeur (0 ou 1) de l'entrée D1. - si CBA = 010 en base 2 => 2 en base 10, alors la sortie Y va prendre la valeur (0 ou 1) de l'entrée D2. ... ainsi de suite jusqu'à : - si CBA = 111 en base 2 => 7 en base 10, alors la sortie Y va prendre la valeur (0 ou 1) de l'entrée D7. Conclusions : La variable /G est en fait une commande qui permet de valider le fonctionnement du multiplexeur : il faut qu'elle soit à 0 pour que le circuit fonctionne en multiplexeur. C'est la commande qui à la priorité la plus haute du circuit (tant qu'elle n'est pas à 0, le multiplexeur ne fonctionne pas !). Une fois cette commande à 0, alors la sortie Y dépend de la valeur de CBA. En fonction de cette valeur, Y va prendre l'état d'une des entrées D0,...,D7. Un mulitplexeur permet donc la sélection de la valeur d'une entrée parmis plusieurs. retour plan 2. Circuits démultiplexeurs et décodeurs 1. Les démultiplexeurs Ces circuit ont 1 entrée. S'ils ont un nombre n de commande, alors ils auront 2^n sorties. Dans notre exemple, nous prendrons un démultiplexeur à 2 commandes (A et B) qui aura donc 2^2 = 4 sorties (Y0,Y1,Y2 et Y3) et une entrée "data". Ce circuit est composé d'un NOR, de 4 NAND et de 4 INVERSEURS : 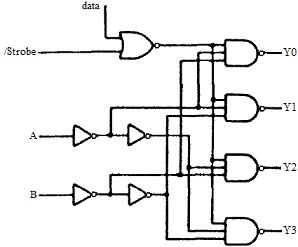
Table de
vérité :
- si /Strobe = 1 alors quelques soient les états de A et B, toutes les sorties sont à 1. - si /Strobe = 0 alors les sorties vont dépendre de l'état des commandes A et B. Si A est le bit de poids fort (valeur 2^1 = 2 en base 10) et B le bit de poids faible (valeur 2^0 = 1 en base 10), alors les sorties varient ainsi : - si AB = 00 en base 2 => 0 en base 10, alors la sortie Y0 prend la valeur de "data" (0 ou 1) et les autres sorties sont à 1. - si AB = 01 en base 2 => 1 en base 10, alors la sortie Y1 prend la valeur de "data" (0 ou 1) et les autres sorties sont à 1. - si AB = 10 en base 2 => 2 en base 10, alors la sortie Y2 prend la valeur de "data" (0 ou 1) et les autres sorties sont à 1. - si AB = 11 en base 2 => 3 en base 10, alors la sortie Y3 prend la valeur de "data" (0 ou 1) et les autres sorties sont à 1. Conclusions : La variable /Strobe est en fait une commande qui permet de valider le fonctionnement du circuit en démultiplexeur. Elle a la priorité la plus importante car tant qu'elle n'est pas à 0, le circuit ne peut pas fonctionner en démultiplexeur ! Une fois cette commande à 0, on se rend compte qu'un circuit démultiplexeur permet de transmettre l'état d'une entrée (ici "data") sur une seule sortie parmis plusieurs. 2. Les décodeurs Si un circuit décodeur à un nombre n de commande, alors il a 2^n sorties. Dans notre cas, nous prendrons comme exemple un décodeur à 3 commandes (A, B et C) et donc 2^3 = 8 sorties (Y0,Y1,...,Y7). Ce circuit est composé de 8 NAND et de 4 INVERSEURS : 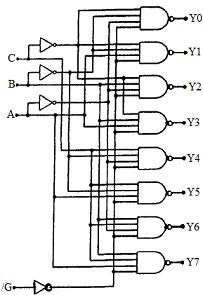 Table de vérité :
Fonctionnement : - si /G = 1 alors quelques soient l'état des commandes, toutes les sorties sont à 1. - si /G = 0 alors les sorties vont dépendre de l'état des commandes A, B et C. Si A est le bit de poids fort (valeur 2^2 = 4 en base 10) et C le bit de poids faible (valeur 2^1 en base 10) alors les sorties varient ainsi : - si ABC = 000 en base 2 => 0 en base 10 alors la sortie Y0 = 0 et toutes les autres sont à 1. - si ABC = 001 en base 2 => 1 en base 10 alors la sortie Y1 = 0 et toutes les autres sont à 1. - si ABC = 010 en base 2 => 2 en base 10 alors la sortie Y2 = 0 et toutes les autres sont à 1. ... - si ABC = 111 en base 2 => 7 en base 10 alors la sortie Y7 = 0 et toutes les autres sont à 1. Conclusions : La variable /G est en fait une commande qui permet de valider le fonctionnement du circuit en décodeur. Elle a la priorité la plus importante car tant qu'elle n'est pas à 0, le circuit ne peut pas fonctionner en décodeur ! retour plan 3. Circuits encodeurs Si un encodeur a un nombre n de sorties, alors il a 2^n entrées. Dans notre exemple nous prendrons un encodeur à 3 sorties (Y2,Y1,Y0), c'est à dire à 2^3 = 8 entrées (e0,e1,e2...,e7). À noter : Gs est aussi une sortie, mais elle n'est pas indispensable. Nous verrons que Gs a un rôle d'encodeur de priorité... Ce circuit comporte 12 ET, 2 NAND, 3 NOR et 12 INVERSEURS : 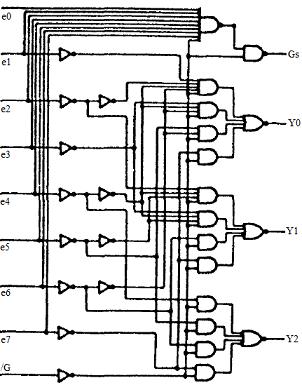 Table de vérité :
Fonctionnement : Considérons, qu'en sortie, Y2 soit le bit de poids fort (valeur 2^2 = 4 en base 10) et que Y0 soit le bit de poids faible (valeur 2^0 = 1 en base 10). - si /G = 1 : quelques soient les entrées, toutes les sorties sont à 1. - si /G = 0 : - si toutes les entrées sont à 1 alors toutes les sorties sont à 1. - si e7 = 0 (et peu importe l'état des autres sorties) alors toutes les sorties sont à 0 (Y2Y1Y0 = 000 en base 2 => 0 = 7-7 en base 10). - si e6 = 0 et e7 = 1 (et peu importe l'état des autres sorties) alors Y0 = 1 et les autres sorties sont à 0(Y2Y1Y0 = 001 en base 2 => 1 = 7-6 en base 10). - si e5 = 0 et les entrées superieures à e5 à 1 alors Y2Y1Y0 = 010 en base 2 => 2 = 7-5 en base 10) ... - dans le cas général : si eN = 0 et les entrées supérieures à eN à 1 alors Y2Y1Y0 sera tel qu'en base 10 il vaudra 7-N. C'est l'encodage réalisé par notre encodeur. Remarque : On peut voir que, lorsque /G = 0, dans le cas où e0e1e2e3e4e5e6e7 = 1111111 et dans le cas où e0e1e2e3e4e5e6e7 = 0111111 alors on a la même sortie Y2Y1Y0 = 111. Alors comment différencier ces 2 états d'entrée puisqu'ils on la même sortie ? On les différencie grâce au bit Gs. En effet dans le cas où toutes les entrées sont à 1 alors Gs = 1 et dans l'autre Gs = 0. Voilà à quoi sert la sortie Gs. On l'appelle encodeur de priorité : il permet de faire la différence entre 2 états d'entrée identiques. Conclusions : La variable /G est en fait une commande qui permet de valider le fonctionnement du circuit en encodeur. Elle a la priorité la plus importante car tant qu'elle n'est pas à 0, le circuit ne peut pas fonctionner en encodeur ! Le circuit étudié peut paraître déjà un peu compliqué et pourtant l'encodage qu'il réalise est plutôt simple. Il existe des encodeurs bien plus complexes puisqu'il existe des codages bien plus tordus ! retour plan 4. Circuits comparateurs et détecteurs d'égalité Ces circuits permettent de comparer la valeurs de 2 entrées. Ces entrées peuvent être écrites sur un ou plusieurs bits. Prenons comme exemple la comparaison de 2 bits "a" et "b" : 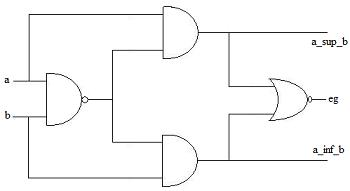 Fonctionnement : - si a > b (<=> a = 1 et b = 0) alors a_sup_b = 1 et eg = a_inf_b = 0. - si a = b alors eg = 1 et a_sup_b = a_inf_b = 0. - si a < b (<=> a = 0 et b = 1) alors a_inf_b =1 et eg = a_sup_b = 0. Remarque : Pour comparer 2 entrées écrites sur plusieurs bits, le principe reste le même. Par exemple si on veut comparer une entrée A sur 2 bits : a1a0 avec une entrée B : b1b0, on va d'abord comparer les bits de poids fort a1 et b1 : - si a1 = 1 et b1 = 0 alors on en déduit immédiatement que A > B sans comparer a0 et b0. - si a1 = 0 et b1 = 1 alors on en déduit immédiatement que A < B sans comparer a0 et b0. - si a1 = b1 alors il faut comparer a0 et b0 de la même façon avant de pouvoir en tirer une conclusion. retour plan |