II. Les différentes familles technologiques de circuits logiques
Page d'accueil
Plan :
I. Les composants à semi-conducteurs
1. La diode
2. Le transistor bipolaire
3. Le transistor JFET
II. Les différentes familles technologiques de circuits logiques
1. L'algèbre de Boole
2. Circuits logiques
à éléments discrets
3. Circuits intégrés logiques DTL
4. Circuits intégrés logiques TTL
5. Circuits intégrés logiques C-MOS
III. Circuits logiques combinatoires
1. Circuits multiplexeurs
2. Circuits démultiplexeurs et décodeurs
3. Circuits encodeurs
4. Circuits comparateurs et détecteurs d'égalité
IV. Circuits logiques séquentiels
1. Bascule RS
2. Bascule D
3. Bascule D à déclenchement par front
4. Bascule JK et JK à déclenchement par front
Par exemple si une tension "créneau" de 0 à +5V est à 5V, on pourra dire qu'on a un 1; mais si elle est à 0V, on dira qu'on a un 0.
Il existe 2 types de logiques :
- la logique positive : quand la grandeur associée au 1 est plus grande que celle associée au 0. En reprenant l'exemple du créneau de tension ci-dessus, on est bien en logique positive car le 5V associé au 1 est évidemment plus grand que le 0V associé au 0 !
- la logique négative : c'est l'inverse ! La grandeur associée au 0 est plus grande que celle associée au 1. En logique négative, pour notre créneau, on aurait un 1 pour 0V et un 0 pour 5V
Ce n'est pas plus compliqué ! Á noter : pour ce cours nous utiliserons la logique positive.
Pour nous aider dans la conception de circuits logiques, nous nous servirons de l'algèbre de Boole. C'est l'algèbre le plus simple du monde, encore plus simple que l'algèbre classique 1+1 =2 !
Nous étudierons donc les principes de cet algèbre, puis les différentes façons de réaliser électroniquement les circuits logiques.
Page d'accueil
Plan :
1. L'algèbre de Boole
2. Circuits logiques à éléments discrets
3. Circuits intégrés logiques DTL
4. Circuits intégrés logiques TTL
5. Circuits intégrés logiques C-MOS
1. L'algèbre de Boole
L'algèbre de Boole permet de comparer des états logiques. Il se compose de trois opérateurs logiques de bases : le ET, le OU et le NON. Rien qu'avec ces 3 opérateurs on peut créer n'importe quel système logique.
1.1 Le ET logique
Aussi appelé AND.
Symbole :
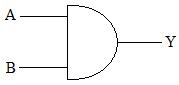
A et B sont les entrées, Y est la sortie.
Principe
:
La relation entre Y, A et B s'écrit : Y = A . B :
- si A = B = 0 alors Y = 0
- si A = 1, B = 0 alors Y= 0
- si A = 0, B = 1 alors Y = 0
- si A = B = 1 alors Y = 1
Autrement dit, la sortie est à 1 si et seulement si toutes les entrées sont à 1.
On peut établir ce tableau récapitulatif (appelé table de vérité) :
Le ET pourra donc servir à tester si toutes les entrées d'un système sont à 1 !
Remarque :
- nous avons étudié un ET à 2 entrées, mais on peut en mettre n'importe quel nombre, le principe restera le même : pour que la sortie soit à 1, il faut que toutes les entrées soient à 1.
retour plan
1.2 Le OU logique
Aussi appelé OR.
Symbole :
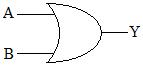
A et B sont les entrées, Y est la sortie.
Principe :
La relation entre Y, A et B s'écrit : Y = A + B :
- si A = B = 0 alors Y = 0
- si A = 1, B = 0 alors Y= 1
- si A = 0, B = 1 alors Y = 1
- si A = B = 1 alors Y = 1
Autrement dit, la sortie est à 1 si au moins une des entrées est à 1.
Table de vérité :
Avec un OU, on pourra donc voir si au moins une des entrées d'un système est à 1.
Remarque :
- on peut mettre autant d'entrées qu'on veut, le principe restera le même : si au moins une entrée est à 1, alors la sortie est à 1.
retour plan
1.3 Le NON logique
Aussi appelé INVERSEUR ou NO.
Symbole :
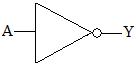
retour plan
1.4 Autres opérateurs...
Il existe d'autres opérateurs dont le fonctionnement pourra être expliqué par la combinaison des 3 opérateurs de base.
Par exemple, étudions l'opérateurs NAND :
La relation entre Y, A et B s'écrit : Y = A . B :
- si A = B = 0 alors Y = 0
- si A = 1, B = 0 alors Y= 0
- si A = 0, B = 1 alors Y = 0
- si A = B = 1 alors Y = 1
Autrement dit, la sortie est à 1 si et seulement si toutes les entrées sont à 1.
On peut établir ce tableau récapitulatif (appelé table de vérité) :
| A | B | Y | |
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Le ET pourra donc servir à tester si toutes les entrées d'un système sont à 1 !
Remarque :
- nous avons étudié un ET à 2 entrées, mais on peut en mettre n'importe quel nombre, le principe restera le même : pour que la sortie soit à 1, il faut que toutes les entrées soient à 1.
retour plan
1.2 Le OU logique
Aussi appelé OR.
Symbole :

Principe :
La relation entre Y, A et B s'écrit : Y = A + B :
- si A = B = 0 alors Y = 0
- si A = 1, B = 0 alors Y= 1
- si A = 0, B = 1 alors Y = 1
- si A = B = 1 alors Y = 1
Autrement dit, la sortie est à 1 si au moins une des entrées est à 1.
Table de vérité :
| A | B | Y | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
Avec un OU, on pourra donc voir si au moins une des entrées d'un système est à 1.
Remarque :
- on peut mettre autant d'entrées qu'on veut, le principe restera le même : si au moins une entrée est à 1, alors la sortie est à 1.
retour plan
1.3 Le NON logique
Aussi appelé INVERSEUR ou NO.
Symbole :

A est l'entrée, Y la sortie.
Principe :
La relation entre Y et A s'écrit : Y = /A :
- si A = 0 alors Y = 1
- si A = 1 alors Y = 0
Autrement dit, la sortie est l'inverse de l'entrée.
Table de vérité :
Principe :
La relation entre Y et A s'écrit : Y = /A :
- si A = 0 alors Y = 1
- si A = 1 alors Y = 0
Autrement dit, la sortie est l'inverse de l'entrée.
Table de vérité :
| A | Y |
| 0 | 1 |
| 1 | 0 |
1.4 Autres opérateurs...
Il existe d'autres opérateurs dont le fonctionnement pourra être expliqué par la combinaison des 3 opérateurs de base.
Par exemple, étudions l'opérateurs NAND :
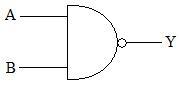
Principe
:
On note Y = /(A.B)
Tout d'abord on peut remarquer que ce symbole est un "mix" entre celui du ET (pour le demi-ovale) et celui du NON (pour le petit rond sur la sortie). Ce "mix" se retrouve aussi dans le nom : NAND <=> NON + AND(ET).
Pour le fonctionnement, c'est la même chose : il s'agit du mélange entre un ET et un NON !
C'est à dire que cet opérateur fonctionne en ET inversé : là où il y avait un 1 en sortie, il y aura un 0; et vice-versa.
On obtient donc la table de vérité du NAND :
On constate donc que dès qu'au moins une entrée est à 0, alors la sorie du NAND est à 1.
Remarques :
- on peut citer d'autres opérateurs :
- le NOR = NON OU. Le NOR aura un fonctionnenment inverse au OU.
- le "OU exclusif" : il fonctionne comme un OU, sauf dans le cas où toutes les entrées sont à 1 car la sortie sera à 0.
retour plan
On note Y = /(A.B)
Tout d'abord on peut remarquer que ce symbole est un "mix" entre celui du ET (pour le demi-ovale) et celui du NON (pour le petit rond sur la sortie). Ce "mix" se retrouve aussi dans le nom : NAND <=> NON + AND(ET).
Pour le fonctionnement, c'est la même chose : il s'agit du mélange entre un ET et un NON !
C'est à dire que cet opérateur fonctionne en ET inversé : là où il y avait un 1 en sortie, il y aura un 0; et vice-versa.
On obtient donc la table de vérité du NAND :
| A | B | Y | |
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
On constate donc que dès qu'au moins une entrée est à 0, alors la sorie du NAND est à 1.
Remarques :
- on peut citer d'autres opérateurs :
- le NOR = NON OU. Le NOR aura un fonctionnenment inverse au OU.
- le "OU exclusif" : il fonctionne comme un OU, sauf dans le cas où toutes les entrées sont à 1 car la sortie sera à 0.
retour plan
2. Circuits logiques à éléments discrets
Ces circuits sont réalisés avec des diodes ou des transistors bipolaires. Prenons comme exemple la réalisation des 3 opérateurs logiques de base.
Réalisation du ET :
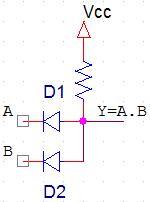
Fonctionnement
:
Considérons que le 1 correpond à la tension Vcc (5V par exemple), et le 0 à la masse : GND (ground) = 0V.
- si A = B = 0 alors les 2 diodes sont polarisées en direct => Elles sont passantes => en Y, on a 0.6V soit environ 0V => Y=0.
- si A = 1, B = 0 alors D1 est polarisée en inverse => D1 est bloquée. En revanche D2 est polarisée en direct => D2 est passante et impose en Y : 0.6V (environ 0V) => Y = 0.
- si A = 0, B = 1 alors de façon symétrique au cas précédent, on a D2 bloquée et D1 passante => Y = 0.
- si A = B = 1 alors les 2 diodes sont polarisées en inverse => en Y on a environ Vcc => Y = 1.
Ce fonctionnement est bien celui d'un ET !
Réalisation du OU :
Considérons que le 1 correpond à la tension Vcc (5V par exemple), et le 0 à la masse : GND (ground) = 0V.
- si A = B = 0 alors les 2 diodes sont polarisées en direct => Elles sont passantes => en Y, on a 0.6V soit environ 0V => Y=0.
- si A = 1, B = 0 alors D1 est polarisée en inverse => D1 est bloquée. En revanche D2 est polarisée en direct => D2 est passante et impose en Y : 0.6V (environ 0V) => Y = 0.
- si A = 0, B = 1 alors de façon symétrique au cas précédent, on a D2 bloquée et D1 passante => Y = 0.
- si A = B = 1 alors les 2 diodes sont polarisées en inverse => en Y on a environ Vcc => Y = 1.
Ce fonctionnement est bien celui d'un ET !
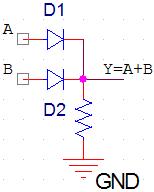
Réalisation du OU :

Fonctionnement
:
0 <=> GND (0V)
- si A = B = 0 alors les 2 diodes sont bloquées => le point Y est lié au GND => Y = 0.
- si A = 1, B = 0 alors D2 est bloquée mais D1 est polarisée en direct => D1 est passante => en Y on a Vcc (Vcc - 0.6 en vrai) => Y = 1.
- si A = 0, B = 1 alors de la même façon on a D1 bloquée et D2 passante => Vcc sur Y => Y =1.
- si A = B = 1 alors les 2 diodes sont polarisées en direct => elles sont toutes les 2 passantes => Vcc sur Y => Y = 1.
Ce fonctionnement est bien celui d'un OU !
Réalisation du NON :
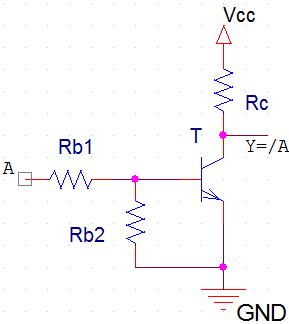
Fonctionnement
:
1 <=> Vcc (5V par exemple)
0 <=> GND (0V)
- si A = 1 alors le transistor T est saturé => Y = Vce_sat = 0.2V = 0 environ (GND) => Y = 0.
- si A = 0 alors le transistor T est bloqué => Y = Vcc => Y = 1.
Ce fonctionnement est bien celui d'un NON !
retour plan
3. Circuits intégrés logiques DTL
DTL = Diode Transistor Logic
Les premiers circuits logiques "évolués" (1959), à base de diodes et de transitors.
Prenons comme exemple la réalisation de l'opérateur NAND :
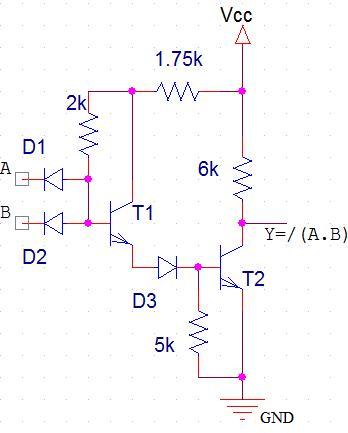
1
<=> Vcc (5V par exemple)
0 <=> GND (0V)
- A = B = 0 : les diodes D1 et D2 conduisent. Par conséquent le courant traversant la résistance de 2 kOhms passe intégralement à travers ces 2 diodes => Ib(T1) = 0 => T1 bloqué => Ib(T2) = 0 => T2 bloqué => V(Y) = Vcc => Y = 1.
- En fait si au moins une des 2 entrées est à 0, alors la diode lui correspondant va être passante ce qui va bloqué T1, puis T2 et Y sera égal à 1.
- A = B = 1 : D1 et D2 sont bloquées => le courant traversant la résistance de 2 kOhms va sur la base de T1 => T1 conduit => on a un courant sur la base de T2 => T2 conduit (saturé) => V(Y) = 0.2 V = 0 environ => Y = 0.
On retrouve bien le fonctionnement d'un NAND : Y = /(A.B) !
Par porte logique (<=> par réalisation d'un opérateur) :
- consommation : 35 mW, important en électronique !
- temps de propagation : 100 ns, lent en électronique !
retour plan
4. Circuits intégrés logiques TTL
TTL = Transistor Transistor Logic
L'élément roi dans ce type de circuits est le transistor bipolaire. Les diodes présentes n'assurent qu'un rôle de protection des circuits (contre les tensions inverses par exemple...).
Réalisation d'une porte NAND :

Remarques :
- les diodes servent à la protection du circuits. Pour l'analyse on pourra faire comme si les diodes D1 et D2 n'existaient pas.
- l'élément T1 est un transistor à 2 emetteurs. Pour l'analyse on a le droit de le remplacer par ceci :
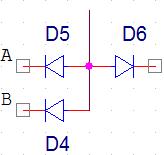
- A = B = 1 :
- Supposons que D6 conduisent => V(K)_D6 = 1.4 V (cf A = B = 0). comme A=B=1, on a V(K)_D4=V(K)_D5=3.6V => D6 a le potentiel de cathode le plus bas, donc elle conduit bien. Notre supposition est vérifiée : D6 conduit tandis que D4 et D5 sont bloquées !
Donc T2 conduit => T4 conduit (on s'arrange pour qu'il sature en pratique) => V(Y) = Vce_sat(T4) = 0.2V => Y = 0.
On retouve bien le fonctionnement d'un NAND !
Par porte :
- consommation : 10 mW
- temps de propagation : 10 ns
retour plan
4. Circuits intégrés logiques C-MOS
Ces circuits sont constitués par des transistors NMOS et PMOS.
Réalisation d'une porte NAND :
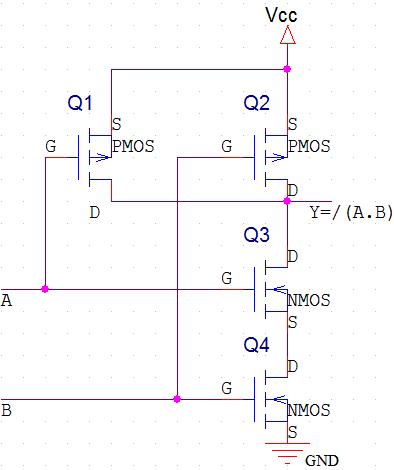
Analyse rapide :
1 <=> Vcc (5V par exemple)
0 <=> GND (0V)
On peut très bien dressé ce tableau pour analyser le fonctionnement du circuit :
On retrouve bien le fonctionnement d'un NAND !
Remarque :
- Q3 étant en amont de Q4, lorsque ce dernier est bloqué (équivalent à un interrupteur ouvert) alors la source de Q3 se retrouve dans un état flottant : on ne peut pas déterminer la valeur de son potentiel. D'où les " ? " dans le tableau. Mais cela n'a aucune influence sur la déterminantion de l'état de la sortie Y.
retour plan
1 <=> Vcc (5V par exemple)
0 <=> GND (0V)
- si A = 1 alors le transistor T est saturé => Y = Vce_sat = 0.2V = 0 environ (GND) => Y = 0.
- si A = 0 alors le transistor T est bloqué => Y = Vcc => Y = 1.
Ce fonctionnement est bien celui d'un NON !
retour plan
3. Circuits intégrés logiques DTL
DTL = Diode Transistor Logic
Les premiers circuits logiques "évolués" (1959), à base de diodes et de transitors.
Prenons comme exemple la réalisation de l'opérateur NAND :

Analyse
rapide :
0 <=> GND (0V)
- A = B = 0 : les diodes D1 et D2 conduisent. Par conséquent le courant traversant la résistance de 2 kOhms passe intégralement à travers ces 2 diodes => Ib(T1) = 0 => T1 bloqué => Ib(T2) = 0 => T2 bloqué => V(Y) = Vcc => Y = 1.
- En fait si au moins une des 2 entrées est à 0, alors la diode lui correspondant va être passante ce qui va bloqué T1, puis T2 et Y sera égal à 1.
- A = B = 1 : D1 et D2 sont bloquées => le courant traversant la résistance de 2 kOhms va sur la base de T1 => T1 conduit => on a un courant sur la base de T2 => T2 conduit (saturé) => V(Y) = 0.2 V = 0 environ => Y = 0.
On retrouve bien le fonctionnement d'un NAND : Y = /(A.B) !
Par porte logique (<=> par réalisation d'un opérateur) :
- consommation : 35 mW, important en électronique !
- temps de propagation : 100 ns, lent en électronique !
retour plan
4. Circuits intégrés logiques TTL
TTL = Transistor Transistor Logic
L'élément roi dans ce type de circuits est le transistor bipolaire. Les diodes présentes n'assurent qu'un rôle de protection des circuits (contre les tensions inverses par exemple...).
Réalisation d'une porte NAND :

Remarques :
- les diodes servent à la protection du circuits. Pour l'analyse on pourra faire comme si les diodes D1 et D2 n'existaient pas.
- l'élément T1 est un transistor à 2 emetteurs. Pour l'analyse on a le droit de le remplacer par ceci :

Finalement, avec toutes ces simplifications, on arrive à ce
circuit équivalent :
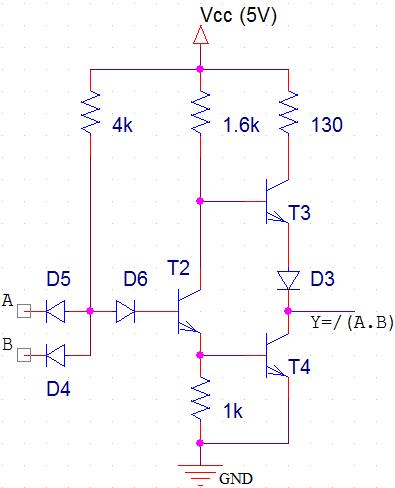
À noter :
- En logique TTL, pour une alimentation Vcc = 5V les niveaux logiques sont référencés par 2 tensions seuils : V0 (0.2V) et V1(3.6V).
Si la tension de sortie V(Y) est inférieure ou égale à V0 alors Y = 0, si V(Y) est supérieure ou égale à V1 alors Y = 1 :
- V(Y) =< 0.2V on a Y = 0
- V(Y) => 3.6V on a Y = 1
- Pour les entrées, on dira qu'une entrée est à 0 si sa tension est de 0.2V et qu'elle est à 1 si sa tension est à 3.6V.
- Les diodes D4, D5 et D6 sont à anodes communes. Donc la diode qui conduit est celle qui aura le potentiel de cathode le plus bas (<=> celle qui sera le mieux polarisée en direct car V(A)-V(K) sera le plus fort).
- A = B = 0 : D4 et D5 conduisent => pas de courant

À noter :
- En logique TTL, pour une alimentation Vcc = 5V les niveaux logiques sont référencés par 2 tensions seuils : V0 (0.2V) et V1(3.6V).
Si la tension de sortie V(Y) est inférieure ou égale à V0 alors Y = 0, si V(Y) est supérieure ou égale à V1 alors Y = 1 :
- V(Y) =< 0.2V on a Y = 0
- V(Y) => 3.6V on a Y = 1
- Pour les entrées, on dira qu'une entrée est à 0 si sa tension est de 0.2V et qu'elle est à 1 si sa tension est à 3.6V.
- Les diodes D4, D5 et D6 sont à anodes communes. Donc la diode qui conduit est celle qui aura le potentiel de cathode le plus bas (<=> celle qui sera le mieux polarisée en direct car V(A)-V(K) sera le plus fort).
- A = B = 0 : D4 et D5 conduisent => pas de courant
Analyse :
- A = B = 0 :
- Supposons que D6 conduise : cela implique que T2 et T4 conduisent aussi => V(K) _D6 = Vbe_T2 + Vbe_T4 = 1.4 V.
Or comme A = B = 0, on a V(K)_D4 = V(K)_D5 = 0.2V : Donc ce sont les diodes D4 et D5 qui on le potentiel de cathode le plus bas => ce sont elles qui conduisent. Donc notre supposition était fausse : D4 et D5 conduisent tandis que D6 est bloquée !
Par conséquent Ib(T2) = 0 => T2 bloqué => Ib(T4) = 0 => T4 bloqué. En revanche T3 conduit :
=> V(Y) = Vcc - Ib(T3)*1.6k - Vbe(T3) - V(D3) = 5 - 1600*Ib(T3) - 0.6 - 0.7 = 3.7 - 1600*Ib(T3) or Ib(T3) est tellement faible en pratique qu'on peut dire que 1600*Ib(T3) est négligeable => V(Y) = 3.7 V => Y = 1.
-En fait si au moins une des 2 entrées est à 0 alors la diode lui correspondant va conduire, et par exactement le même raisonnement on aura Y=1.
- A = B = 0 :
- Supposons que D6 conduise : cela implique que T2 et T4 conduisent aussi => V(K) _D6 = Vbe_T2 + Vbe_T4 = 1.4 V.
Or comme A = B = 0, on a V(K)_D4 = V(K)_D5 = 0.2V : Donc ce sont les diodes D4 et D5 qui on le potentiel de cathode le plus bas => ce sont elles qui conduisent. Donc notre supposition était fausse : D4 et D5 conduisent tandis que D6 est bloquée !
Par conséquent Ib(T2) = 0 => T2 bloqué => Ib(T4) = 0 => T4 bloqué. En revanche T3 conduit :
=> V(Y) = Vcc - Ib(T3)*1.6k - Vbe(T3) - V(D3) = 5 - 1600*Ib(T3) - 0.6 - 0.7 = 3.7 - 1600*Ib(T3) or Ib(T3) est tellement faible en pratique qu'on peut dire que 1600*Ib(T3) est négligeable => V(Y) = 3.7 V => Y = 1.
-En fait si au moins une des 2 entrées est à 0 alors la diode lui correspondant va conduire, et par exactement le même raisonnement on aura Y=1.
- A = B = 1 :
- Supposons que D6 conduisent => V(K)_D6 = 1.4 V (cf A = B = 0). comme A=B=1, on a V(K)_D4=V(K)_D5=3.6V => D6 a le potentiel de cathode le plus bas, donc elle conduit bien. Notre supposition est vérifiée : D6 conduit tandis que D4 et D5 sont bloquées !
Donc T2 conduit => T4 conduit (on s'arrange pour qu'il sature en pratique) => V(Y) = Vce_sat(T4) = 0.2V => Y = 0.
On retouve bien le fonctionnement d'un NAND !
Par porte :
- consommation : 10 mW
- temps de propagation : 10 ns
retour plan
4. Circuits intégrés logiques C-MOS
Ces circuits sont constitués par des transistors NMOS et PMOS.
Réalisation d'une porte NAND :

Analyse rapide :
1 <=> Vcc (5V par exemple)
0 <=> GND (0V)
On peut très bien dressé ce tableau pour analyser le fonctionnement du circuit :
| A B | Vgs_Q1 Q1 | Vgs_Q2 Q2 | Vgs_Q4 Q4 | Vg_Q3 Vs_Q3 | Vgs_Q3 Q3 | V(Y) Y |
| 0 0 | -5V conduit | -5V conduit | 0 bloqué | 0 ? | ? ? | Vcc 1 |
| 0 1 | -5V conduit | 0 bloqué | 5V conduit | 0 0 | 0 bloqué | Vcc 1 |
| 1 0 | 0 bloqué | -5V conduit | 0 bloqué | 5 ? | ? ? | Vcc 1 |
| 1 1 | 0 bloqué | 0 bloqué | 5V conduit | 5 0 | 5V conduit | 0 0 |
Remarque :
- Q3 étant en amont de Q4, lorsque ce dernier est bloqué (équivalent à un interrupteur ouvert) alors la source de Q3 se retrouve dans un état flottant : on ne peut pas déterminer la valeur de son potentiel. D'où les " ? " dans le tableau. Mais cela n'a aucune influence sur la déterminantion de l'état de la sortie Y.
retour plan